Estimating the time-of-arrival is a common problem in a wide range of settings, e.g. in logistics. This post will show a distribution-based approach that enables us to get more insights about arrival times and how we could use this information for decision making in the logistics industry.
Problem Setup
In times of Google maps the estimation of expected times of arrival has become a common thing in everyday lives. Point estimators give us a single time of arrival and we assume or at least hope, that this estimated time will be as accurate as possible.
As this is most of the times sufficient for private purposes, it lacks information for industry solutions and decision making. Storing stock is expensive and companies try to keep it as small as possible. On the other side missing parts can stop whole production lines and missing goods may lead to unhappy customers.
For these use-cases more information is required to answer questions like, in which time window will our cargo arrive with a n-percent probability (quantiles), how sure are we that the goods will arrive at that day +/- n-days and so on. To answer that kind of questions we need a time-of-arrival distribution rather than a point estimator.
If the final result is supposed to be a distribution we have to be careful not to lose too much information on our way there. In logistics we often have switches of cargo between different modes of transfer or between different instances of the same mode of transport. If we want to get a bunch of smartphones from Shenzhen in China to Karlsruhe in Germany we may go by Truck from the factory to the airport, by airplane to Frankfurt and then by railway to Karlsruhe. If it is a really large amount of phones and we have more time, we might also go by truck from Shenzhen to Shanghai, take a container ship to Rotterdam, change to another container ship to Hamburg and go from there by railway to Karlsruhe.
Looking at these examples, it becomes clear that we can not use a single model to derive our final result and that we might have different options for transportation.
If we used point estimators on our way and only estimate a distribution for our final leg, we might lose a lot of information. A much better approach would be to derive arrival distributions for each leg and chain them together to derive one final distribution. This is the approach we developed together with one of our customers.
A Little Introduction to Distributions
To understand the way we are propagating distributions through our routes, some basic knowledge about probability theory is required. If your are familiar with those concepts skip this section or take it as a short reminder.
When talking about distributions in our context we usually mean probability mass functions (pmf). The sum over a pmf is always one and the value inside each discrete bin, representing a point in time in our case (or to be more precise a time range of the width of the bin), represents the probability of occurrence.
If we convolve two pmfs the result will be a pmf again, representing the sum of the underlying random variables. Using this property we can derive the probability distribution of a specific event given the probability distribution of a previous event. This principle is closely related to bayesian networks. The easiest way to show this is by using the Dirac function for one of the pmfs . The Dirac function has a value of one for one specific value and is zero otherwise. Thereby it represents the case where we have a 100% chance of occurrence, e.g. for an event that already happened.
If we convolve a Dirac function with an arbitrary pmf it will shift the pmf by the shift of the Dirac. So if we were 100% certain that we reach our intermediate location after 3 days and we have a pmf modeling the time of arrival for the second leg (neglecting the transfer between different modes) we could just convolve them and end up with a leg two arrival distribution that is shifted by 3 days.
If we had two equally probable options we could use two Dirac impulses scaled by 0.5 and multiply them with our pmf. This would result in two scaled and shifted versions of our pmf that sum up to one and thereby form a pmf again.
As we add more and more scaled Dirac points we end up with a pmf, so this also holds for convolving two pmfs.
Routing Considerations and Notation
If we think about a time-of-arrival distribution over multiple transfer locations, we could model the problem as a Directed Acyclic Graph (DAG). In this DAG the edges represent connection between different locations via the possible modes of transport and the nodes represent transfers between different modes of transport or different instances of the same mode of transport. This representation helps to think about our problem in a visual manner.
Each edge in our graph is characterized by a start and an end location, a mode of transport and a the time of arrival pmf for this specific leg. Graph edges might appear and vanish over time and the pmf for the same edge will probably change over time due to seasonal effects.

Each node in our graph represents a transfer point, where our cargo will change the vehicle. It is characterized by its location and the incoming and outgoing mode of transport. Each node has to model the time between the time-of-arrival at the port and the time-of-departure from the port. It also has to take into account the fact that we might miss our follow up vehicle and need to take an alternative.
As a notation we mark routes by consecutive legs chained to each other by arrows. Staying with our previous example of phones we get
China Shenzhen -> Deutschland Frankfurt -> Deutschland Karlsruhe
Because these countries and cities might have lengthy names we will write them in the UN/LOCODE standard with the first two characters defining the country and the last three characters defining the city. So our route will look like
CNWUH -> DEFRA -> DEKAE
If we know the mode of transport for the specific leg we will name it in brackets insight the arrow.
CNSNZ -(AIR)> DEFRA -(RAIL)> DEKAE
In case we have some time information given, e.g. the start date, we add it before or after the arrow.
CNSNZ {15.04.2020}-(AIR)> DEFRA -(RAIL)> DEKAE
To visualize alternative routes we could use brackets again.
CNSNZ [
{15.04.2020}-(AIR)> DEFRA -(RAIL)> DEKAE |
{15.04.2020}-(SEA)> NLROT -(SEA)> DEHAM -(RAIL)> DEKAE
]
Looking at this notation it becomes clear that routing can be arbitrarily complex. So we need a quite sophisticated routing algorithm with access to a lot of distinct information and domain knowledge, or we need to restrict our choice of alternatives by some simplifying rules. In our case we will assume that we always already have the whole route including a start date and we are not allowed to change the route, even if we miss our follow up vehicle.
Deriving the Building Blocks
In our Graph model we have two main building blocks: nodes and edges. The underlying idea is to derive one type of machine learning model for each building block. For each model type we can have several instances to modulate different modes of transport.
Edges (Direct Leg Model)
For the Edges we decide for one model per mode of transport that gives us a time-of-arrival pmf. This can be derived by a regression or multi-class classification model. For regression we have to normalize our result to sum up to one, for the classification model we are interested in the resulting probability per class and not the argmax() of this distribution.
Nodes (Transfer Model)
The nodes are a bit more difficult. They model the time it takes to move the cargo from one vehicle to the other, so the easiest way would be to train a transfer time model for each mode of transport combination. However, this would assume that our follow up vehicle is already there, waiting for our cargo. As this might be true for modes of transport such as truck, it is rarely true for other modes of transport such as rail, sea or air. As they will carry cargo from many different sources, they will behave more like a bus and leave on a predefined schedule, not waiting for delayed cargo. In such cases the delayed cargo has to take the next possible instance that is allowed with respect to business constraints. In our case we will assume that we have to stay at least on the same mode of transport, which is quite realistic.
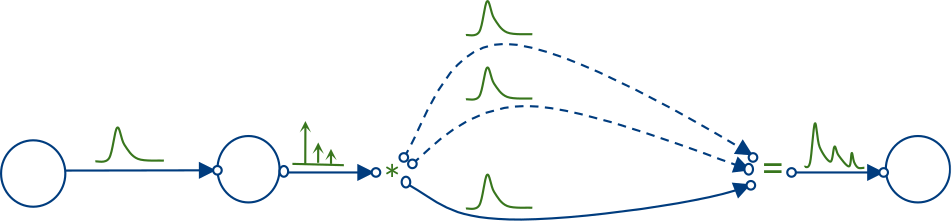
If we assume that we have access to the schedules of our transport vehicles, we could derive a node model that takes into account cases where the cargo misses its follow up vehicle. Assuming for simplicity that our follow up vehicles depart on time, we could model them as a sequence of scaled Dirac impulses which sum up to one and thereby again form a pmf. The time shift of the Dirac impulses models the schedule while the scaling factor is derived by the node model and represents the probability of reaching this vehicle instance given the time-of-arrival distribution at the node.
Assembling the Parts
Given a full route with the aforementioned restrictions we can now calculate a final time of arrival pmf. We start with our defined start date at Shenzhen.
CNSNZ {15.04.2020}-(AIR)> DEFRA -(RAIL)> DEKAE
As a first step we call our direct air leg model for our current date, starting at Shenzhen and landing at Frankfurt. The result will be a pmf which we mark by f(base date).
CNSNZ {15.04.2020}-(AIR)>{f(15.04.2020)} DEFRA -(RAIL)> DEKAE
Based on this arrival pmf and the schedule information, the transfer model will result in a range of follow up vehicle instance options, modeled by scaled Dirac impulses, with probabilities of occurrence summing up to one.
CNSNZ {15.04.2020}-(AIR)>{f(15.04.2020)} DEFRA {0,6*20.04.2020, 0,4*22.04.2020}-(RAIL)> DEKAE
For each of the base dates we can evaluate our second direct leg model and convolve it with its corresponding Dirac. If we add these distributions element-wise we end up with our final pmf. Note, if we assume that the direct leg model would give the same result for each base date, we could just convolve the output of our node model with the pmf of our leg model.
CNSNZ {15.04.2020}-(AIR)>{f(15.04.2020)} DEFRA {0,6*20.04.2020, 0,4*22.04.2020}-(RAIL)>{sum(0,6*f(20.04.2020), 0,4*f(22.04.2020))} DEKAE
Our simplification to stay on the same route also has the big advantage that we end up with exactly one Distribution on the arrival at a node. Without these restrictions our route could fork into multiple options which would require some extra considerations.
Use Case Scenarios
Resulting Metrics
With the chaining of complete routes at hand we have build a powerful analysis framework that can be used to answer multiple questions regarding the arrival of cargo. The first and most obvious one is to take the mean or maximum of the final time-of-arrival pmf as a point estimator for the predicted time-of-arrival. However, if we were only interested in this, we probably could have achieved it easier.
More interestingly, we can now calculate the percentage of cases where we arrive in a specific time window (two sided quantiles), or up to a specific point in time (one sided quantiles). This is not only useful for risk management, it also gives us a possibility to calculate the costs of being late. If you know that running out of stock on a specific good will cost you a defined amount of money per day and you also know your storage costs for the same good, the quantiles of the time of arrival pmf can tell you the most cost-efficient point in time to order new stock.
Or if you are a logistics company and you want to give guaranteed time windows of arrival, you can calculate how often you will not be in time and set the extra fees for your guarantee accordingly.
Configurations for Different Requirements
Having talked about what you can do with the result of our framework, there are different use-case-specific ways to get to the final pmf. Staying with the case where we know our route and the time-of-departure at the starting point, we could apply the same concept to track our cargo on its way with updated data. If we know that our cargo just departed from our first transfer node we could recalculate our final distribution with the new information. This would remove uncertainty from our final result and we might have time to take appropriate measures if we see that our first prediction does not hold anymore.
In case, we do not know our time of departure we could just take all scheduled departures with our desired mode of transport from our starting location in the next n-days, calculate a final distribution for each possible departure date and average over them. The result will be a bit fuzzier, but might be sufficient for several use cases.
There are probably many more options to use this setup by changing the restrictions and adding more or less concrete information. Obviously, results get better the more information we have about our route and the corresponding transport vehicles but this requires that we have this information available (and in time).
Possible issues: Talking About Data
When implementing such a framework, there are several issues that make life a bit harder than plain theory might suggest. The first problem that is probably common to all data products is the shortage and lack of trustworthiness of ground truth data. To train the required node and leg models, a sufficient amount of correct training data is required. However, we probably have a lot of data sources or long chains of external data aggregation beyond our control, as we require data for different modes of transport that usually belong to different companies.
The amount of data for specific legs will also vary widely between main routes, side routes and new routes where we have no data at all. This is the main reason we need a stochastic model, that can infer information from routes where we have much data to the routes where we only have sparse or even no data. On the other side this will lead to situations where our models might have a bias towards characteristics of main routes.
This problem is closely related to the combinatorial explosion that we have. In our example we assumed that we have a specific route given and thereby strongly restricted the space of options at a transfer point. If we want to allow different paths to the same destination we need a router with a huge amount of data and of domain knowledge. This router does not only need to know which modes of transport we have available at each node, it also needs to know which ones the specific cargo is allowed to take based on domain specific business rules.
Another problem that we need to handle is that our models are living in the past. The predictions are based on historical data, but the time-of-arrival might be impacted by seasonal or transient effects. We have to include such information as good as possible in our model training. Also the router and models need to be updated regularly, as new connections might arise while old ones might be removed.
Conclusion
The framework discussed here is the base of an advanced analysis setup for time-of-arrival analysis. It can provide useful insights in the logistic setups of different kinds of companies. By leveraging or restricting assumptions and inserting business knowledge into models and routers it can be customized to serve the individual needs. This tool works by inferring missing information about a connection on a stochastic base and chaining this information together for a final solution. Thereby it is quite flexible and can also return results if only sparse data is provided. Flexibility is also induced by the modular structure of the framework that allows to switch models and combination strategies easily if we learned something new or reality changed.
However, results need to be taken with a grain of salt as we will always get a final distribution, no matter how sparse and wrong our amount of input information is. We need to be careful not to get blinded by the fact that our result looks like it contains a lot of information. To verify how trustful the result is, other measures about the quality of the underlying data, schedules, etc should be taken into account to get some sort of prediction reliability. It is required that end consumers understand the strength and weaknesses of this framework when they use it. But when they do, it can be a powerful support for decisions and lead to a highly improved transparency in logistics processes.



